|
|
|
Close Help | ||||||||||||||
 |
 |
1. Schema výpočtu
2. Postup výpočtu
3. Posloupnost zatěžovacích stavů
4. Předpis nenulových posunutí
5. Specifikace výpočtového modelu
6. Řídící parametry řešiče HDYN

1) příprava výpočtu: Řešení nelineární dynamické úlohy musí předcházet
příprava jako pro lineární výpočet až do sestavení matice tuhosti podle
kapitoly LINEÁRNÍ ELASTOSTATICKÁ ÚLOHA a dále sestavení
matice hmotnosti programem HMOT. V nelineárních
výpočtech platí následující pravidla:
i) Použít se mohou jen isoparametrické prvky s lineární tvarovými
funkcemi, tj. bez středových uzlů hran (ref. A1-A7).
ii) Nelze využít obecné periodicity.
iii) Materiálové vlastnosti se zadají podle kapitoly MATERIÁLOVÉ
VLASTNOSTI a podle (ref. D).
iv) Při definici zatěžovacích stavů v souboru name.i2
se postupuje podle odstavce 3. Posloupnost zatěžovacích
stavů v této kapitole.
program: RMD2/3, RPD2/3, SRH2/3, HMOT
vstupy: name.i1, name.i2,
name.i3,
name.iM,
protokol: name.o1, name.o2,
name.o3,
name.oM,
výstupy: binární soubory
detaily: kapitola LINEÁRNÍ ELASTOSTATICKÁ
ÚLOHA, referenční příručka - VSTUPY, přílohy A,B,C,D
2) zadání historie zatížení a výpočtového modelu: Vstupní data se zapíší v ASCII formátu do souboru name.iP. Při definici historie zatížení se postupuje podle odstavce 3. Posloupnost zatěžovacích stavů v této kapitole. Pokud již nelineární výpočet proběhl (tj. úloha byla úspěšně vyřešena programem HDYN), lze připojit další zatížení pomocí KREST = 2 - viz 3. Posloupnost zatěžovacích stavů.
program: HPP2 (2D úloha), HPP3 (3D úloha)
vstupy: name.iP + binární soubory z předchozích
výpočtů
protokol: name.oP
výstupy: binární soubory
detaily: odstavce 3. Posloupnost zatěžovacích
stavů a
5. Specifikace výpočtového modelu
v této kapitole, referenční příručka - VSTUPY/name.iP
3) řešení soustavy rovnic: Vstupní data se zapíší v ASCII formátu do souboru name.iN. Algoritmem řešení je metoda centrálních diferencí KMET = 1. Poslední iterace ukončeného řešení je automaticky použita jako výchozí aproximace pro nový běh programu. Před opětovným spuštěním programu HDYN je možné (ale nikoliv nutné) změnit vstupní data v souboru name.iN.
program: HDYN (2D i 3D úloha)
vstupy: name.iN + binární soubory z předchozího
výpočtu
protokol: name.oN
výstupy: binární soubory (řešení je v name.PLS)
detaily: odstavec 6. Řídící parametry řešiče
HDYN v této kapitole, referenční příručka - VSTUPY/name.iN
4) výpočet napětí a deformací: Vstupní data se zapíší v ASCII formátu do souboru name.i5, přičemž KPROB = 2. Vždy se musí zadat číslo ILC s ohledem na skutečný počet vyřešených stavů - viz 6. Řídící parametry řešiče HDYN. Při nastavení klíče KGRAF = 1 se vytvoří ASCII soubor name.STR s výstupy pro grafický postprocesor GFEM. V tomto souboru je efektivní plastická deformace označena jako SCALAR1 a efektivní creepová deformace jako SCALAR2.
program: STR2 (2D úloha), STR3 (3D úloha)
vstupy: name.i5 + binární soubory (řešení je v
name.PLS)
protokol: name.o5
výstupy: name.STR
detaily: odstavec 6. Řídící parametry
řešiče HDYN v této kapitole, referenční příručka - VSTUPY/name.i5
3. Posloupnost zatěžovacích stavů
Odezva nelineárních materiálů závisí nejen na velikosti a směru působících sil, ale také na pořadí v jakém jsou zatěžovací účinky přikládány. Proto je třeba zadat časový sled zatížení. Vycházíme z obvyklého pojmu "zatěžovací stav," kterým máme na mysli teplotu a veškeré síly působící na těleso v daném časovém okamžiku. Definice všech zatěžovacích stavů, jež budou využity v nelineárním výpočtu, se provádí standardně programem RPD2/3. Z takto předem připravených zátěží se potom pomocí programu HPP2/3 vybere a sestaví posloupnost potřebná pro modelování historie zatížení, jak je schematicky znázorněno na následujícím obrázku.
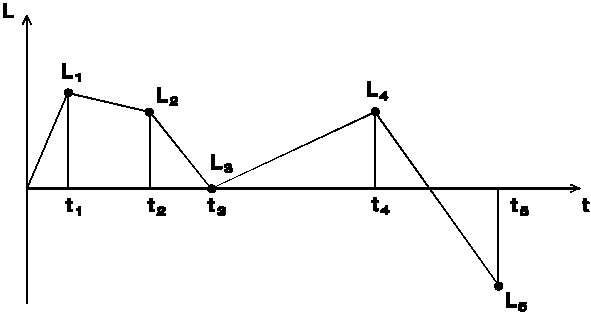
Automaticky se přitom předpokládá, že přechod z Li do Li+1 probíhá rovnoměrně z hlediska deformací. Tento přechod mezi jednotlivými stavy je sice velmi blízký rovnoměrné změně zatížení, nemusí být však vždy totožný. Proto v případech, kdy je třeba bezpodmínečně dodržet silovou zatěžovací cestu, je nutné příslušný úsek rozdělit na menší přírůstky. Zatěžovacím stavem, který je předepsaný, soustava prochází za všech okolností.
K dosažení jemnějšího dělení není nutno zadávat další zatěžovací stavy; jednoduchou možnost poskytuje program HDYN. Ve většině případů je však zbytečné sahat k podobným opatřením, protože zpomalují výpočet (zpravidla zbytečně). Přesnost integrace konstitutivních rovnic je zabezpečena jiným způsobem a v případě creepu těleso prochází rovnovážným stavem na konci každého časového přírůstku.
Zatěžovací stavy se definují následujícím způsobem:
1) V souboru name.i2 se v rámci dávky
AS 1 (tj.
v prvním přiřazení) běžným způsobem definuje materiál, nulová posunutí
uzlů, eventuální předpis pružin a výchozí teplota tělesa. Dále uvedená
zatížení (tlak, osamělé síly atp.) se berou v úvahu jen v lineárním výpočtu.
Pro nelineárních úlohy se zatěžovací účinky popsané v AS 1 nedají
využít a je nutné je zadat v AS 2 a výše. V přiřazení /R 0 To
Tw/ má význam jen počáteční teplota To, odpovídající
stavu bez napětí. Hodnota Tw se neuplatní. Popřípadě se zadají
páry kontaktních ploch.
2) V dávkách AS 2, AS 3, ... se postupně vytvoří všechny zatěžovací
stavy, které budou použity v nelineárním výpočtu. Jejich pořadí je prozatím
nevýznamné. Zatížení se nezadává přírůstkově, ale absolutně (vzhledem k
nule). Jestliže se například vyskytne přiřazení /R 0 To Tw/,
vzniká zatěžovací stav, ve kterém má těleso teplotu Tw [oC].
Hodnota To je ignorována.
3) Vstupní data se zpracují programem RPD2/3 a dále se provede výpočet
matic tuhosti (SRH2/3) a eliminace soustavy (FEFS). Možné je též vypočítat
elastická napětí pomocí STR2/3.
4) Sestaví se posloupnost zatěžovacích stavů L1, L2,
..., kde čísla
Li jsou pořadová čísla
AS dávek.
Např. L2 = 5 znamená, že druhý zatěžovací stav byl definován
v AS 5 (aktuální přírůstek oproti minulé konfiguraci je L2
- L1). Pokud se dodatečně ukáže, že některý zatěžovací stav
chybí, je nezbytné celou úlohu přepočítat od bodu 2).
5) V souboru name.iP se na IP řádku zadá
IP 1 NLC NCYC KMOD KCRP KLARG KCNT 3*0L1
L2 ... LNLC
NLC počet členů zatěžovací posloupnosti
NCYC počet cyklů (opakování celé posloupnosti); default=1 celkový počet
řešených stavů je NCYC*NLC
KMOD, KLARG, KCNT - viz 5. Specifikace výpočtového modelu
6) Pro úlohu je nutné zapsat koncové časy výpočtu odpovídající
všem zatěžovacím stavům. To se provede na RP řádku:
RP 10*0 t1 t2 ... tNLC
Časy se zadávají ve stejných jednotkách jako časový krok v řešiči HDYN.
Předpokládá se tNLC > ... > t2 > t1
> 0 a NCYC je vždy 1 (je možné též zapsat NCYC = 0).
7) Vstupní data se zpracují programem HPP2/3 a nelineární dynamická
úloha se spočítá řešičem HDYN. Pokud řešení proběhlo úspěšně, můžeme navázat
v bodě 5) zadáním dodatečných zatěžovacích stavů, které však musely být
definovány předem v rámci AS dávek v souboru name.i2
(návrat k bodu 2) znamená přepočítání
celé úlohy). V souboru name.iP
stačí zapsat na první posici IP řádku hodnotu klíče restartu KREST
= 2:
IP 2 NLC NCYC KMOD KCRP KLARG KCNT 3*0
L1
L2 ... LNLC
U úloh se přirozeně předpokládá, že první čas t1
je větší nebo roven času, ve kterém bylo ukončeno předchozí řešení. V opačném
případě program HPP2/3 hlásí chybu. Restartu KREST = 2 je možno
využít pro řešení úloh s předpětím. Nejprve se vypočítá předpětí při KREST
= 1 (např. zbytková pnutí po procesu chladnutí) a pak se odstartuje nová
série zatížení (např. cyklického) s
KREST = 2. Tímto způsobem se
dá pracovat s materiálovými vlastnostmi, které jsou změněny předchozí historií.
poznámka: U 2D problémů se nenulová rovinná deformace ezo
(ref. name.i2) při KSS = 1 (ref.
name.i1)
nesmí měnit v průběhu zatěžování. Tzn. zatěžovací stav s přiřazením
/R
0 0 0 ezo/ se smí vyvolat jen
jako L1.
4. Předpis nenulových posunutí
V nelineárních úlohách připouští systém PMD jen jediný způsob jak vynutit
nenulové posunutí (deformační zatížení). Tím je metoda pokutové funkce
- penalty. Uvažujme část sítě na obrázku, kdy je uzlu předepsán posuv uo.
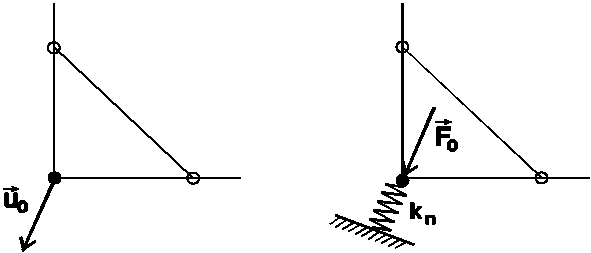
Zvolenému uzlu se nejprve přiřadí pružina o tuhosti kn ve směru daném vektorem uo (kapitola ULOŽENÍ TĚLESA, 6. Předpis pružin v této příručce, VSTUPY name.i2 a příloha B6 v referenční příručce). Tuhost kn by měla být přibližně o 6 řádu vyšší, než je lokální tuhost tělesa (což lze alespoň řádově odhadnout). Dále se přiřadí uzlová síla Fo = knuo, která vynutí na pružině posuv uo. Protože je tuhost pružiny podstatně větší než-li tuhost tělesa, dá se očekávat, že i skutečný posuv bude blízký uo.
Podle odstavce 3. v této kapitole se definují všechny potřebné pružiny
v dávce
AS 1 a adekvátní uzlové síly v dávkách AS 2 a vyšších.
Jestliže zatěžovací stav Li obsahuje diskretní sílu F
v uzlu s velmi tuhou pružinou, znamená to, že ve stavu Li
bude vynucen posuv u = F/kn. Pokud v některém
zatěžovacím stavu chybí předpis takové síly, bude posuv uzlu přibližně
nulový.
5. Specifikace výpočtového modelu
Volba výpočtového modelu vyplývá z materiálových vlastností popsaných
v souboru name.i2, popř. name.DAT
a ze vstupních parametrů v name.iP (ref.
VSTUPY, přílohy B5,
B6,
D).
elastoplasticita: Model plasticity se volí parametrem
KMOD,
který se zadává v souboru name.iP na IP řádku.
IP KREST NLC NCYC KMOD
KCRP KLARG KCNT 3*0 L1 L2
... LNLC
KMOD = 1 von Misesův model - J2 teorie (default)
KMOD = 2 zobecněný asociovaný model
KMOD = 3 zobecněný neasociovaný model
Zvolenému modelu musí odpovídat materiálové vlastnosti podle (ref.
D).
Význam ostatních parametrů na IP řádku je vysvětlen v odstavci
3.
Posloupnost zatěžovacích stavů.
RP řádek se vynechá.
creep: Hodnota KMOD = 0.
KCRP = 0 bez creepu
KCRP = 1 standardní creep dle PMD - v souboru name.i2
se zadá závislost ![]() podle (ref. D).
podle (ref. D).
KCRP = 21x,22x,23x Binův model creepu typ 2a),2b),2c)
KCRP = 2x1,2x2,2x3 Binův model - deformace, čas, poškození
Pro Binovi modely creepu se popis creepových vlastností materiálu čte
ze souboru name.DAT.
elastoplasticita + creep: Postupuje se podle předchozího.
Zadá se parametr KMOD rozlišující plastické modely a parametr KCRP
rozlišující creepové modely. Kombinovaný výpočet je vhodné spustit až po
odladění separovaných problémů.
geometricky nelineární úloha: aktivuje se při KLARG
= 1 (velké rotace, malé deformace - totální Lagrangeovská formulace).
kontaktní úloha: aktivuje se při KCNT = 1. V name.i2
se musí zadat páry kontaktních ploch jako SV dávky s KQT 10 a 11, 12 a
13 atd. V name.iL je nutno nastavil hodnotu penalty PENAL.
6. Řídící parametry řešiče HDYN
Řídícím parametrem úlohy je zvolený integarční krok metody centálních diferencí. Metoda je podmínečně stabilní.
IP KMET KPOUT 2*0 NINT KTPR
RP 3*0 PENAL TSTEP BETA
KMET metoda řešení
KMET = 1 metoda centrálních diferencí (default)
KPOUT Klíč výstupu. V závorkách je uveden výsledný počet vektorů řešení
(zatěžovacích stavů), které se objeví v binárním souboru name.PLS.
Těmto vektorům pak v programu STR2/3 odpovídá pořadové číslo ILC
(ref. VSTUPY/
name.i5). Pokud byla úloha
restartována s KREST = 2 (viz odstavec 3. Posloupnost
zatěžovacích stavů), soubor name.PLS se přepíše (řešení
z předchozího běhu se musí zpracovat před restartem).
KPOUT = 0 Kontrola vstupních dat (0).
KPOUT = 1 Po každém zatěžovacím stavu (NCYC*NLC).
KPOUT = 2 Po každém cyklu (NCYC).
KPOUT = 3 Jen výsledné řešení (1).
NINT Dělení integračního intervalu (default = 10). Parametr NINT souvisí s přesností řešení. Řádová chyba v napětích je podstatně menší než 100/NINT [%]. Defaultová hodnota dává ve většině případů malou chybu (cca 1-3%) a nedoporučuje se ji proto měnit. Při řešení creepových úloh je časový krok programem HDYN nastavován automaticky. Položení NINT = 1 má za následek vyřazení krokovacího algoritmu z činnosti (připouští se 100% lokální chyba). U elastoplastických úloh může integrace s NINT = 1 významně urychlit výpočet, aniž by se příliš poškodilo řešení. Integrační metoda se pak redukuje na algoritmus prediktor - korektor (Euler forward - radial return).
KTPR Výstup na display a do protokolu name.oN.
KTPR = 0 Žádný výstup.
KTPR = 1 Trasování výpočtu (doporučeno).
KTPR = 2 Trasování + vektor posunutí po každé iteraci.
KTPR = 3 Trasování + vektor reakcí uložení.
Na RP řádku se zadávají:
PENAL velikost penalty [N/m^3] (pouze pro dynamické kontaktní
úlohy)
TSTEP velikost integračního kroku pro centrální diference
[s]
BETA parametr pro speciální tvar Rayleighovy matice
tlumení C=BETA*M.
Počáteční podmínky se zadávají na IC řádku ve třech možných tvarech:
IC ISET T KQT R LSOL-čísel
- čte počáteční vektor délky LSOL
nebo
IC ISET T KQT I IREC
- čte počáteční vektor délky LSOL ze souboru name.SOL, kde IREC je
číslo rekordu v tomto souboru
nebo
IC ISET T KQT R NDIM-čísel
- čte složky konstantního počátečního vektoru ve směru souřadnicových
os, kde NDIM je dimense úlohy.
ISET pořadové číslo dávky
KQT klíč počátečních podmínek
KQT = 1 počáteční posunutí
KQT = 2 počáteční rychlost
Poznámka: pokud není IC dávka definována, automaticky se předpokládá, že jsou počáteční podmínky homogenní
Výpis veličin v zadaných uzlech v každém integračním kroku je možné zadat na IN řádku
IN ISET T KPRIN I seznam uzlů
ISET pořadové číslo dávky
KPRIN klíč tisku veličin v uzlech
KPRIN = 1 tiskne posunutí
KPRIN = 2 tiskne posunutí a rychlost
KPRIN = 3 tiskne posunutí, rychlost a zrychlení.
Příklad:
;KMET KPOUT 2*0 NINT KTPR
IP 0 1 2*0
0 0
;3*0 PENAL TSTEP BETA
RP 3*0 0 0.031 0
IC 1 T 2 R 0 0 -1
IN 1 T 3 I 1:8
EN
EN
 |
 |