Model studies of deep nuclear waste repository
Study of physical and chemical processes in components of DGR for high-level waste (HLW) and spent nuclear fuel (SNF) is one of the main applications of the Research centre’s results. Currently our work mostly concerns numerical simulations. Laboratory experiments are planned and performed in 2007 year and in-situ tests are performed with collaboration of our partners. For the simulations we develop our own codes besides the standard software. We cooperate with several institutes in the Czech Republic and also we participate in an international project.
In the Czech Republic, the Radioactive Waste Repository Authority (RAWRA - SURAO) is responsible for the design and construction the repository and coordination of the needed R&D activity, including the direct financial support.
Currently we specialize on the following problems (links to abstracts and examples of results):
- modelling of flow and transport processes in fractured rock – development and tests of finite-element code based on a multidimensional (porous-fracture) concept
- simulations of in-situ borehole hydraulic tests in granite massifs (Potucky and Melechov sites, projects of Czech geological survey)
- thermomechanical simulations with parallel computer codes (in cooperation with Institute of Geonics)
- bentonite coupled heat and moisture transport (code developments and simulation of laboratory experiments)
The list of both finished and running projects and contracts (from newest)
- Research of near-field processes of the deep geological repository of spent nuclear fuel and high-level waste, contract of Czech Radioactive Waste Repository authority (RAWRA) for consortium of TUL/ARTEC, Czech Technical University, Institute of Chemical Technology, lead by Nuclear Research Institute Řež
- Task Force on Engineered Barrier System (EBS) – project coordinated by SKB, participation by means of contract of RAWRA
- Geological and other work on the test site Melechov (granitic massif), part Mathematical modelling of fluid flow in fractured media of a test site, contract of RAWRA, subcontract from Czech geological survey
- SB/660/2/03, Development of a method of in situ identification and mathematical modelling of flow and geochemical interaction in fractured matrix of compact rocks, Ministry of Environment 2003-2005
- GA205/00/0480, Migration of radionuclides and toxic compounds in fractured matrix of crystalline massif, Grant Agency of the Czech Republic 2000-2002
- SB/630/3/00, Complex geochemical research of interaction and migration of organics and inorganics compounds in rock environment, Ministry of the Environment 2000-2002
- GA205/96/0921, Mathematical modelling of the transport and the reactions of the chemical substances in the contaminated underground water, Grant Agency of the Czech Republic 1996-1999
The list of both finished and running projects and contracts (from newest):
- Research of near-field processes of deep repository of spent nuclear fuel and high-level waste, contract of Czech Radioactive waste repository authority (RAWRA) for consortium of TUL/ARTEC, Czech technical university, Institute of chemical technology, lead by Nuclear research institute Řež
- Task Force on Engineered Barrier System (EBS) – project coordinated by SKB, participation by means of contract of RAWRA
- Geological and other work at test site Melechov massif, part Mathematical modelling of fluid flow in fractured media of a test site, contract of RAWRA, subcontract from Czech geological survey
- SB/660/2/03, Development of a method of in situ identification and mathematical modelling of flow and geochemical interaction in fractured matrix of compact rocks, Ministry of environment 2003-2005
- GA205/00/0480, Migration of radionuclides and toxic compounds in fractured matrix of crystalline massif, Grant agency of the Czech Republic 2000-2002
- SB/630/3/00, Complex geochemical research of interactoins and migratins of organics and inorganics compounds in rock environment, Ministry of environment 2000-2002
- GA205/96/0921, Mathematical modelling of the transport and the reactions of the chemical substances in the contaminated underground water, Grant agency of the Czech Republic 1996-1999
Publications:
- O. Severýn, M. Hokr, J. Královcová, J. Maryška, Modeling of groundwater flow and contaminant transport in hard rock using multidimensional FEM/FVM, GeoProc2006 Advances on Coupled Thermo-Hydro-Mechanical-Chemical Processes in Geosystems and Engineering, HoHai University, Nanjing, China, 2006, pp. 356–363.
- Vohralík M., Maryška J., Severýn O., Mixed and nonconforming finite element methods on a system of polygons, Appl. Numer. Math., In press
- Maryška J., Severýn O., Vohralík M., Numerical simulation of fracture flow with a mixed-hybrid FEM stochastic discrete fracture network model, Comput. Geosci. 8 (2004), 217–234.
- Maryška J., Severýn O., Rukavičková L.: Data management and data-mining for numerical modelling in the complex hydrogeological projects. VIIth IAHS Scientific Assembly, Foz do Iguacu, 2005.
- Maryška J., Severýn O., Rukavičková L.: Hydrogeological processes in a compact rock massif – a New Approach to the Numerical Modelling. Eurock 2005 (P. Konečný ed.), Leiden, 2005.
- M. Hokr and J. Havlíček: Comparison of multidimensional and dual-porosity models of solute transport in fractured rock, Proceedings of SIMONA 2006, Technical university of Liberec, pp. 54-61.
Modeling of flow and transport processes in fractured rock
Mathematical description and theory of mixed-hydrid finite elements on the multidimensional (combined continuum and discrete fracture network) domain for the fluid flow problem – download paper
Mathematical description of the transport problem on the multidimensional domain (combined dual porosity continuum and discrete fracture network) – download paper
The basic idea of multidimensional model application results from the following facts:
- it is not possible to represent real structure of all fractures in larger scale, e.g. with the class of discrete fracture network (from both data availability and computational reasons)
- the equivalent continuum models are inappropriate simplification for detailed and coupled studies
- both large conductive fractures and small fractures are important either for the hydraulics or for the solute retention
- there is important role of large fracture intersections, behaving like ''pipe''
The combination of discrete and continuum models is now implemented in several finite element codes (e.g. FEFLOW, CONNECTFLOW) but there are still many limitations and open questions concerning, e.g. the generation of discretisation mesh for both 3D, 2D and 1D elements or the availability of appropriate input data.
 |
| Principle of the numerical discretisation of the multidimensional model – connection of 3D continuum and 2D and 1D discrete fracture network elements. |
 |
| Difference between conforming (compatible) and non-conforming (incompatible) connection of continuum and fracture elements. |
 |
 |
| Relation between real fracture network and multidimensional model: the hydraulically
important fractures are represented explicitly while the small fractures are represented as continuum (possibly double-continuum for the dual-porosity transport model) |
|
 |
|
| Scheme of the solution algorithm for the solute transport problem. We consider the multidimensional model and each part composed of mobile and immobile zone (dual-porosity continuum and dual-porosity fractures) |
|
 |
 |
 |
| Ratio=500 | 50 | 5 |
 |
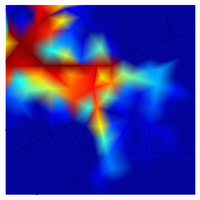
| Examples of solute transport in a combination of 2D continuum and 1D discrete fractures for variable ratio of fracture and continuum hydraulic conductivity. |
Simulations of in-situ borehole hydraulic tests in granite massifs
 |
| Discrete fracture network in the Potucky site model – hydraulic communication of two boreholes. |
 |
| Results of piezometric head in the fracture network during a particular test |
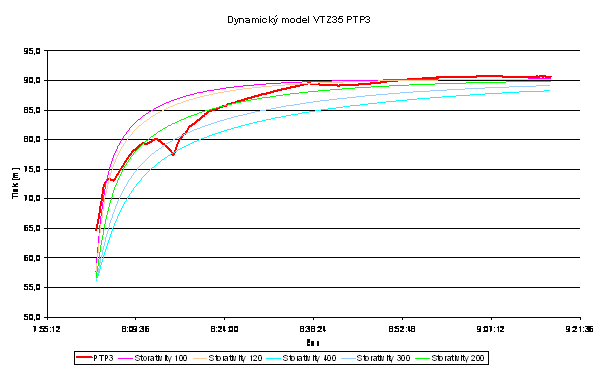 |
| Results of the fitting the time-pressure measured curve with various values of storativity (thick uneven lin e is the measurement) |
 |
| Scheme of the Melechov site |
 |
 |
| Results of the Melechov site hydraulic simulation: piezometric head and velocity | |
Thermo-mechanical simulations with parallel computer codes
The results are obtained in cooperation with Institute of Geonics, Academy of Sciences of the Czech Republic, Ostrava (UGN). We present a model solution of heat conduction and stress field around the repository.
The problem characteristics:
- disposal boreholes, galleries and canisters (packagings) dimensions, as well as the waste heat production according to the Czech reference repository project
- reference physical parameters of steel, bentonite and granite
- sample of the repository structure is modeled, using symmetry assumption
- domain dimensions 31.62 x 58.0 x 99.77 m
The numerical parameters:
- discretisation with structured hexahedral mesh, 145 x 105 x 50 nodes, 761250 degrees of freedom for the heat conduction, 2283750 d.o.f. for the elasticity problem
- simulation time 200 years, automatic time stepping, beginning at 0.0008yrs, ending at 13.1072yrs
Computer equipment for parallel simulations at UGN:
- workstation IBM xSeries 455 (symmetric multiprocessor – SMP, 8 processors) with 64-bit processors Intel Itanium2 1.3 GHz
- PC cluster THEA with 8 computer nodes AMD Athlon 1.4 GHz, 1.28 GB RAM.
 |
 |
| Global FEM mesh | Mesh detail at the disposal place |
Results:
 |
 |
 |
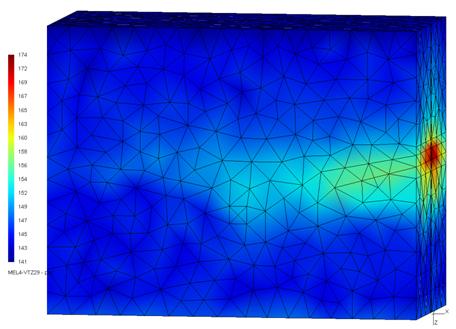
| Temperature distribution at the time 14 years (maximum) – various cross-sections and a detail. | ||
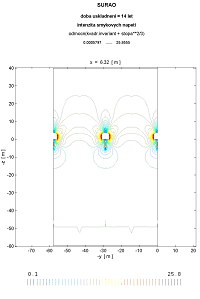 |
 |
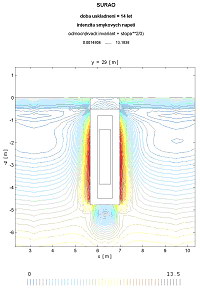 |
| Shear stress intensity | ||
Bentonite coupled heat and moisture transport
We use an alternative model of water distribution in bentonite, which is appropriate for the situation without contact with liquid water, like the moistrure redistribution driven by heat gradient. Water is assumed to be in two phases, gas (vapor) in the pores as mobile part and sorbed on solids as immobile part. The equilibrium is given by the adsorption isotherm, sorbed water mass ratio as a function of air relative humidity. For the situation without liquid water, this model replaces the standard use of retention curve extrapolated from the case of liquid water and capillary forces.
 |
| Illustration of water distribution to the mobile (air) and immobile (bentonite solid grains) zone, with non-equilibrium exchange determined by the adsorption isotherm. |
 |
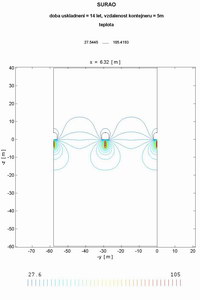
| Scheme of the experiment solved in the EBS Task Force project. Position of the temperature sensors. |
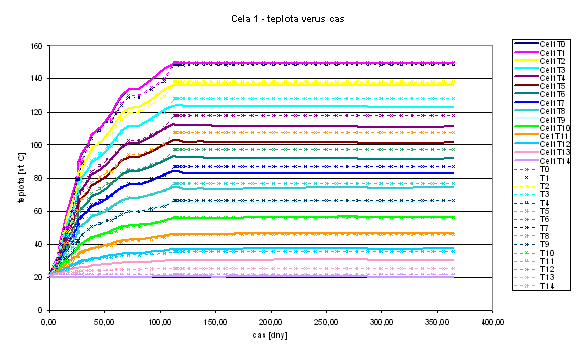 |
| Fitting of the temperature distribution in the space and time (model versus measurement) |
 |
| Fitting of the relative humidity distribution in the space and time (model versus measurement) |
