Mar APR May 5 2013 2014 2015
1 capture 5 Apr 14 - 5 Apr 14

Close Help

  
Edge traction, BEAM61S1

Problem description: The cantilever beam shown is subjected to uniformly distributed loading l_y, l_z per unit length and the end force F_x, F_y, F_z. Calculate deflection and stresses for two load cases: i) the in-plane problem using l_y, F_x, F_y only and ii) the complete three-dimensional loading l_y, l_z, F_x, F_y, F_z.

Mesh: Four semi-loofs--see appendix B.2.

Material properties: $E=2\times 10^5$ MPa, $\nu=0.3$.

Support: Clamped at x=0. Statically determinate.

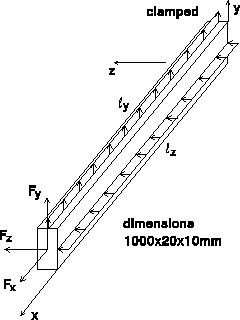
u=v=w=0 node: 		 1 
u=w=0 node: 		 2 


$u=w=\alpha=\beta=0$ node:            11

Loading: Given as

ly=-100 lz=200 unit: N/m 
Fx=20000 Fy=-20 Fz=10 unit: N      

Solution: The end force is replaced with the equivalent edge traction as

$$l_x=\frac{20000}{0.02}=1000\times 10^3\,\mbox{[N/m]}~,~~~ l_y=-10^3\,\mbox{[N/m]} ~,~~~ l_z=0.5\times 10^3\,\mbox{[N/m]}$$

The distributed loading in y direction is transformed to the local coordinate systems of the elements edges L2 that coincide with the line $y=0.02\,,~z=0$. According to numbering shown in appendix B.2, we have

$$l_{xh}(\verb*\vert L2\vert)=l_y=-100\,\mbox{[N/m]}$$

for all the elements 1 to 4.

The distributed loading in z direction is replaced with the normal surface traction q_n acting on the only semi-loof's face S1 . This is carried out in the same way as in example II.4, therefore

$$q_n(\verb*\vert S1\vert)=-\frac{l_z}{0.02}=-0.01\times 10^6\,\mbox{[Pa]}$$

Execute from prompt:
>rmd3 beam61s1.I1
>rpd3 beam61s1.I2
>srh3 beam61s1.I3
>fefs beam61s1.I4
>str3 beam61s1.I5