Fyzikální ústav Akademie věd ČR

Nanoparticles (NPs) are very often viewed as the bulk-like material and their internal alignment is neglected. The main conjunction of the ideal NP with the corresponding bulk substance is that both are homogeneous within their whole volume, which means that any material parameter is constant within all unit cells of both the bulk and NP.

However, experiments demonstrate that there are significant differences in the crystal and spin structure of the real NP with respect to the bulk-like case and as a consequence, corresponding material parameters vary within the NP volume (see Fig. 1). Typical example is the canting of the surface spins or different crystallinity and spin order within the NP core and shell, respectively [1-3]. This results in decrease of the saturation magnetization, M_S with increasing magnetic disorder in the NP or significant variation of the NP diameters determined by different methods (d_TEM, d_XRD, d_MAG, see Fig. 1).

Fig.1.: The example of typical experiments for determination of the properties of magnetic nanoparticles: a) Powder X-ray Diffraction pattern from which the phase composition and the particle diameter (d_XRD) are determined. b) Transmission Electron Microscopy, which is used for direct observation of the apparent particle size (d_TEM) and its distribution. c) Example of Mӧssbauer spectra. Refinement of spectra can easily distinguished between the presence of the Fe²⁺ and Fe³⁺ ions, thus method serves for precise determination of the maghemite/magnetite phase content within the examined sample. Bottom panel: Magnetic property measurements: d) example of the ZFC-FC curve from which the blocking temperatures, T_MAX and T_irr can be determined. e) Example of the M(H) curve and f) the fit of the unhysteretic M(H) curve in Langevin scaling from which the mean and meadian magnetic moments of the particles can be obtained together with the distributions of magnetic moment. g) Illustration of the internal particle structure for the ideal and real particles and relation of individual particle diameters.

In our work, we focused on quantification of the NP internal structure and introduced formalism which treated level of single-particle disorder (details in [4]).

Moreover, the spin-canting phenomena was examined in detail [5]. Monodisperse maghemite nanoparticles with diameter ranging from 7 to 20 nm were examined by the In-field Mӧssbauer Spectroscopy (IFMS) in varying external magnetic field up to 6 T. Surprisingly, the small-sized particles (7 nm) exhibited nearly no spin canting in contrast to the larger particles with lower surface-to-volume ratio. It was demonstrated that the observed phenomenon is originated by lower relative crystallinity of the larger particles with different internal structure.

Single-particle internal structure is affected also by the interparticle inetractions and is manifested in the particle effective anisotropy. We demonstrated for the systems of the CoFe₂O₄ NPs embedded in SiO₂ matrix that magnetic response of such concentrated NP systems could be explained by the concept of modified NP effective anisotropy rather than by the strength of the interparticle interactions [6] , as was usually done. We observed that characteristic parameters of the single-domain state (coercivity, µ₀H_c and blocking temperature, T_B) and dipole-dipole interaction energy (E_d-d) of the samples were proportional with each other and increased with increasing (d_XRD/r)³, where d_XRD was the NP diameter and r was the interparticle distance. Our results were in excellent agreement with the Monte-Carlo simulations of the particle growth [7]. Moreover, we presented that behavior of the systems was not sufficiently interpreted either by the E_d-d acting as an additional energetic barrier to the superspin reversal, or average static field acting on a single NP. Changes of the blocking temperature and coercivity with respect to the non-interacting superparamagnetic regime were then attributed to the reformed relaxations of the NP superspins due to the interactions and modified effective anisotropy energy of the interacting NPs.

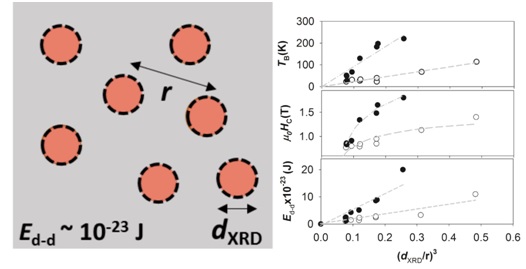
Fig.2: Example of the dependence of blocking temperature, T_B, coercivity, µ₀H_c and energy of dipole-dipole interactions,E_d-d on the (d_XRD/r)³, where d_XRD is the particle diameter and r is the interparticle distance for the nanoparticles embedded in insulating SiO₂ matrix.

References:
[1] S. Blundell, Magnetism in Condensed Matter, 1st ed., vol. 4. Oxford University Press, New York, 2001.
[2] J.M.D. Coey, Phys. Rev. Lett. 27 (1971) 1140.
[3] S. Morup, E. Brok, C. Frandsen, J. Nanomater. 2013 (2013) 720629.
[4] B. Pacakova, S. Burianova, M.P. Morales, G. Salas, J. Vejpravova, Universal parameter of spin and structural disorder of single-domain nanoparticles for biomedical applications, submitted.
[5] S. Kubickova, D. Niznansky, M. P. Morales Herrero, G. Salas, J. Vejpravova, Structural disorder versus spin canting in monodisperse maghemite nanocrystals, Appl. Phys. Lett. 104 (2014) 223105.
[6] B. Pacakova, A. Mantlikova, D. Niznansky, S. Kubickova, J. Vejpravova, Size and distance driven competition of interparticle interactions and effective anisotropy , J. Phys. Cond. Mater. , submited.
[7] D. Kechrakos, K.N. Trohidou, Phys. Rev. B 58 (1998) 12169.