Lidé
Beneš Pavel, Ing., odborný pracovník
Bryscejn Jan, Ing., Laboratoř optických metod, odborný pracovník
Cacciotti Riccardo, Mgr., Laboratoř optických metod, doktorand
Fiala Zdeněk, RNDr., CSc., zástupce ředitele pro výzkumm, vědecký pracovník
Kafka Vratislav, Ing., DrSc., vědecký pracovník
Koudelková (Petráňová) Veronika, Mgr., Laboratoř optických metod, doktorandka
Minster Jiří, Ing., DrSc., vědecký pracovník
Valach Jaroslav, Ing. Ph.D., vedoucí Laboratoře optických metod, vědecký pracovník
Vavřík Daniel, Dr., Ing., vedoucí oddělení, vědecký pracovník
Popis činnosti
Oddělení mechaniky kontinua se zabývá mechanikou materiálů s ohledem na popis jeho chování během zatěžování a to jak z teoretického tak i z experimentálního hlediska. S ohledem na současný stav poznání se výzkum zaměřuje především na nelineární fyzikální děje, kdy je pro jejich věrohodný popis třeba charakterizovat celou historii zatěžování (nestačí tedy znát pouze výchozí a konečný stav objektu). Nelinearity se projevují například při porušování houževnatých těles, které je doprovázeno rozvojem lomové procesní zóny a rozsáhlou plastizací; nelineární popis elastických vzorků je nutný v případě velkých deformací s komplikovanou historií zatěžování; zdrojem nelinearit je výrazně heterogenní struktura těles, což platí především pro stavební materiálu či vláknové kompozity; mezi nelineární děje patří i dlouhodobé fyzikální procesy, pozorované například u termoplastů; do oblasti zájmu oddělení patří I vysoce nelineární materiály s tvarovou pamětí. Věrohodný teoretický popis nelineárního chování materiálů je nutné podepřít experimentálně, v oddělení je proto zásadní pozornost věnována i vývoji a implementaci pokročilých experimentálních metod a souvisejícího hardwarového i softwarového vybavení. Součástí oddělení mechaniky kontinua je laboratoř optických metod.
Výzkum
Experimentální sledování rozvoje poškození a trhliny v houževnatém materiálu – analýza naměřených dat
V rámci oddělení byla vyvinuta experimentální metodika, využívající nástrojů obrazové korelace dat. Je tak možné během zatěžování tělesa s trhlinou sledovat rozvoje pole deformací. Při znalosti konstitutivních rovnic zkoumaného materiálu můžeme vypočítat i příslušná napětí, plastické přetvoření a lomově mechanické parametry jako je otevření trhliny či J integrál. Zároveň byla rozvinuta metodika radiografického a tomografického sledování lomové procesní zóny (s využitím RTG záření) – pro tyto účely jsou používány specializované zatěžovací stroje vyvinuté v ústavu.

Vzorek umístěný v kompaktní zatěžovacím stroji je během zatěžování sledován optickou kamerou a zároveň je pomocí RTG záření sledován rozvoj poškození/trhliny.
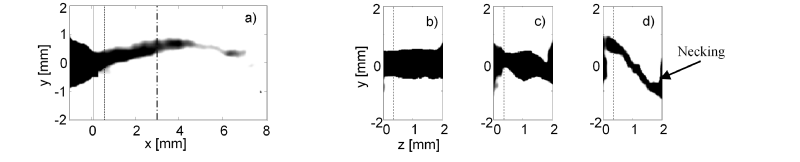
Příklad rozvoje trhliny, identifikované pomocí tomografické rekonstrukce. Vlevo je vidět její tvar ve střední části vzorku, vpravo jsou příklady tří příčných řezů – je patrné její stáčení z původní roviny.

Vlevo je intenzita plastické deformace, vypočtená přímo z experimentálních dat. Uprostřed intenzita napětí při maximální zatěžovací síle a vpravo napětí po nárůstu trhliny (došlo k relaxaci napětí).
Geometrie konečných deformací a časová inkrementální analýza deformačních procesů:
V souvislosti se vznikem výpočtové mechaniky a následným rozvojem inkrementálních metod vyvstal v mechanice přetvárných těles nový problém – totiž jak v rámci konečných deformací správně linearizovat a integrovat deformační procesy v časové proměnné. Protože dosavadní postupy nevedly k uspokojivým výsledkům, řešíme tuto problematiku nově pomocí geometrického přístupu. Ten vychází z formulace mechaniky přetvárných těles jako jednoduchého lagrangeovského systému nad konfiguračním prostorem deformačních tenzorů, který je reprezentovaný prostorem symetrických pozitivně definitních reálných matic Sym+(3,R) s netriviální geometrií. Deformační tenzory jako základní veličiny popisující konečné deformace spojitého prostředí totiž určují délky a úhly mezi vektory u deformovaného stavu a jsou proto reprezentovány symetrickými pozitivně definitními maticemi. Oproti tomu, jejich aproximace pomocí tenzorů malých deformací (přesněji infinitezimálních) jen představují korekci výchozí konfigurace pomocí tenzorových polí, které jsou reprezentovány jen symetrickými maticemi tvořícími pouhý vektorový prostor. V případě konečných deformací je situace složitější. Ačkoliv se poloha i tvar deformovaného tělesa realizují v běžném třídimenzionálním euklidovském prostoru, odpovídající časový průběh deformačního tenzoru sleduje trajektorii v neeuklidovském prostoru – záporně zakřiveném (globálně) symetrickém Riemannově prostoru Sym+(3,R). Geometrie tohoto prostoru pak slouží jako východisko zmíněného přístupu, který umožňuje využít k analýze deformačních procesů nástroje diferenciální geometrie a teorie Lieových grup. Výsledkem je mimo jiné geometrická interpretace logaritmického tenzoru přetvoření, geometricky konzistentní linearizace deformačních procesů (včetně časové derivace napětí), jakož i identifikace evoluční rovnice Lieova typu pro konečné deformace umožňující geometricky konzistentní časovou integraci nelineárních konstitutivních vztahů v rámci konečných deformací, která platí obecně, bez ohledu na konkrétní materiálové konstitutivní vztahy.

Schematické zobrazení vztahů mezi veličinami popisující konečné deformace (B je těleso před deformací, S1 a S2 jsou po sobě následující jeho deformace)
Hodnocení vlivu dlouhodobého stárnutí polymerních kompozitních materiálů
Hodnocení vlivu dlouhodobého stárnutí polymerních kompozitních materiálů na jejich základní mechanické vlastnosti užitím akcelerovaných metod. Izolované degradační mechanismy jsou pro jednotlivé materiály popsány hojně v odborné literatuře, avšak možné synergické efekty dosud nejsou dostatečně známy a pochopeny. Dvě základní metody zahrnují akcelerované zkoušení a akcelerované stárnutí. Pro prvou možnost, tj. akcelerované zkoušení, je důležité odvodit rovnocennost mezi průběhem a výsledky zkoušek s požadovanou servisní dobou. Akcelerované zkoušení je požadováno pro mechanismy, které jsou spojeny s rostoucí akumulací nepříznivých změn (poškození nebo deformací), které mohou vést přímo k poruše.
Akcelerované stárnutí je používáno k vytvoření situace blízké ke konečnému stavu mikrostruktury nebo porušení zkoušeného materiálu pro následující charakterizační testy. Zde je důležitá důvěra, že mikrostrukturální či vlivem urychleného stárnutí poškozený stav odpovídá předpokládanému nebo pozorovanému stavu před ukončením životnosti. Obě metody jsou a budou používány k hodnocení změn mechanického chování vybraných polymerních kompozitních materiálů vystavených definovaným účinkům dlouhodobého působení mechanických, fyzikálních a chemických vlivů.
Projekty
Nelineární lom konstrukčních materiálů – zkoumání projevů disipace energie v zóně porušení pomocí pokročilých experimentů a modelování (2015-2017)
Diagnostika poškozování a životnosti objektů kulturního dědictví (2011-2015)
Energetické a napjatostní aspekty kvazikřehkého lomu – důsledky pro určování lomově-mechanických parametrů silikátových kompozitů (2009-2012)
Přechod od mikro- a nano-indentačních dat získaných instrumentovaným měřením k mechanickým charakteristikám vazkopružných materiálů (2008-2010)
Publikace
Fíla, T.; Zlámal, P.; Jiroušek, O.; Falta, J.; Koudelka_ml., P.; Kytýř, D.; Doktor, T.; Valach, Jaroslav. Impact testing of polymer-filled auxetics using Split Hopkinson Pressure Bar. Advanced Engineering Materials. 2017, ISSN 1438-1656.
Jandejsek, Ivan; Gajdoš, Lubomír; Šperl, Martin; Vavřík, Daniel. Analysis of standard fracture toughness test based on digital image correlation data. Engineering Fracture Mechanics. 2017, roč. 182, September, s. 607-620. ISSN 0013-7944. http://www.sciencedirect.com/science/article/pii/S0013794417305799
Fiala Zdeněk, Geometry of finite deformations and time-incremental analysis, International Journal of Non-Linear Mechanics. 2016, Roč. 81, May, s. 230-244, ISSN 0020-7462, 2016, http://www.itam.cas.cz/publications/priv/0456940.pdf
Vokoun, David; Sysel, P.; Heller, Luděk; Kadeřávek, L.; Svatuška, Michal; Goryczka, T.; Kafka, Vratislav; Šittner, Petr. NiTi-polyimide composites prepared using thermal imidization process. Journal of Materials Engineering and Performance. 2016, roč. 25, č. 5, 1993-1999. ISSN 1059-9495.
Fiala Zdeněk, Evolution equation of Lie-type for finite deformations, time-discrete integration, and incremental methods, Acta mechanica. 2015, Roč. 226, č. 1, s. 17-35, 2015, http://www.itam.cas.cz/publications/priv/0428756.pdf
Fiala Zdeněk, Discussion of On the interpretation of the logarithmic strain tensor in an arbitrary system of representation by M. Latorre and FJ Montans, International Journal of Solids and Structures. 2015, 56/57, March, s. 290-291, 2015, http://www.itam.cas.cz/publications/priv/0440201.pdf
Kafka Vratislav, Vokoun David, A three-scale model of basic mechanical properties of Nafion, Mechanics of Composite Materials. 2015, Roč. 50, č. 6, s. 763-776, 2015, http://www.itam.cas.cz/publications/priv/0441356.pdf
Kafka Vratislav, Relations among the crack growth modes resulting from tensor splitting, Acta Technica CSAV. 2015, Roč. 60, č. 4, s. 319-335, 2015, http://www.itam.cas.cz/publications/priv/0453491.pdf
Minster Jiří, Králík V., Temperature-dependent microindentation data of an epoxy composition in the glassy region, Mechanics of Time-Dependent Materials. 2015, Roč. 19, č. 1, s. 75-85, 2015, http://www.itam.cas.cz/publications/priv/0441600.pdf
Kumpová, Ivana; Fíla, Tomáš; Vavřík, Daniel; Keršner, Z. X-ray dynamic observation of the evolution of the fracture process zone in a quasi-brittle specimen. Journal of Instrumentation. 2015, roč. 10, č. 8, C08004. ISSN 1748-0221. http://iopscience.iop.org/1748-0221/10/08/C08004/pdf/1748-0221_10_08_C08004.pdf
Vavřík, Daniel; Jandejsek, Ivan. Experimental evaluation of contour J integral and energy dissipated in the fracture process zone. Engineering Fracture Mechanics. 2014, roč. 129, October, s. 14-25. ISSN 0013-7944. http://www.sciencedirect.com/science/article/pii/S0013794414000988



