
Vedoucí laboratoře: Ing. Radek Kolman, Ph.D.
Laboratoř výpočetní mechaniky těles se zabývá analýzou nelineárních statických a dynamických problémů v rámci metody konečných prvků v oborech kontaktu a rázu deformovatelných těles doprovázených geometrickými a materiálovými nelinearitami. Dále je předmětem zájmu šíření vln v heterogenních a neizotropních prostředích analytickými i numerickými metodami a vyhodnocování a porovnávání modelů MKP s experimentálními výsledky. Kromě tohoto je věnováno značné úsilí studiu defektů v krystalických materiálech metodou molekulární dynamiky i experimentálně a výpočtu elektronických struktur a celkových energií neperiodických systémů metodou konečných prvků nebo pseudopotenciálem.
 PMD je moderní výpočetní soubor programů na základě metody konečných prvků (MKP), který je nezávislý na platformě. Systém je určen pro všeobecné inženýrské problémy v mechanice kontinua tuhých těles. Jde o proprietární kód s dlouhou, 35letou tradicí, který je v současnosti udržován a vyvíjen zaměstnanci Laboratoře výpočetní mechaniky těles. Další informace o systému PMD naleznete zde.
PMD je moderní výpočetní soubor programů na základě metody konečných prvků (MKP), který je nezávislý na platformě. Systém je určen pro všeobecné inženýrské problémy v mechanice kontinua tuhých těles. Jde o proprietární kód s dlouhou, 35letou tradicí, který je v současnosti udržován a vyvíjen zaměstnanci Laboratoře výpočetní mechaniky těles. Další informace o systému PMD naleznete zde.
Řešitelé: J. Plešek, J. Novotný, J. Dobiáš, S. Pták, D. Gabriel, P. Pařík, R. Kolman, Z. Hrubý, J. Kopačka, V. Sháněl, R. Marek
Spolupráce: VAMET, s.r.o.
 Projekt je zaměřen na výpočtové modelování šíření vln v tělesech a heterogenních prostředích. Cílem je zpřesnění existujících MKP modelů pro řešení přechodových dějů v různých oblastech, které spojuje šíření napěťových vln. Hlavním předmětem výzkumu je studium dispersních vlastností rovinných kvadratických serendipity prvků včetně optimalizace diagonalizačních metod pro tyto typy prvků, přesnosti a stabilitě numerických integračních schémat. Zvláštní pozornost je věnována šíření vln v silně heterogenních médií, víceškálovému modelování a homogenizaci, nelinárnímu vysokorychlostnímu impaktu a šíření zvukových vln v předepjatém prostředí.
Projekt je zaměřen na výpočtové modelování šíření vln v tělesech a heterogenních prostředích. Cílem je zpřesnění existujících MKP modelů pro řešení přechodových dějů v různých oblastech, které spojuje šíření napěťových vln. Hlavním předmětem výzkumu je studium dispersních vlastností rovinných kvadratických serendipity prvků včetně optimalizace diagonalizačních metod pro tyto typy prvků, přesnosti a stabilitě numerických integračních schémat. Zvláštní pozornost je věnována šíření vln v silně heterogenních médií, víceškálovému modelování a homogenizaci, nelinárnímu vysokorychlostnímu impaktu a šíření zvukových vln v předepjatém prostředí.
Řešitelé: D. Gabriel, J. Plešek, R. Kolman, J. Červ, F. Valeš, J. Dobiáš
Spolupráce: Fakulta aplikovaných věd, Západočeská univerzita v Plzni
Související publikace:
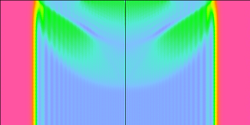 Projekt se zabývá počítačovým modelováním rázových kontaktních úloh. Hlavním cílem projektu je vývoj původního trojrozměrného algoritmu založeného na pre-diskretizačním přístupu včetně souvisejících metod. Součástí projektu je i analýza numericky stabilních metod pro lokální vyhledávání kontaktu. Navržený algoritmus je implementován do explicitního řešiče, který je součástí programového souboru PMD.
Projekt se zabývá počítačovým modelováním rázových kontaktních úloh. Hlavním cílem projektu je vývoj původního trojrozměrného algoritmu založeného na pre-diskretizačním přístupu včetně souvisejících metod. Součástí projektu je i analýza numericky stabilních metod pro lokální vyhledávání kontaktu. Navržený algoritmus je implementován do explicitního řešiče, který je součástí programového souboru PMD.
Řešitelé: D. Gabriel, J. Plešek, J. Kopačka, P. Pařík, R. Kolman, V. Sháněl, Z. Hrubý
Spolupráce: Ústav konstrukcí a návrhů strojů, Fakulta strojní, Univerzita v Mariboru, Slovinsko
Související publikace:
 Cílem projektu je vývoj a aplikace originálních moderních numerických metod vhodných pro vysocevýkonné počítače s některými vynikajícími vlastnostmi (numerická a paralelní škálovatelnost) pro výpočty v mechanice tuhé fáze při řešení silně nelineárních problémů. Počítačové kódy jsou vyvíjeny v rámci MKP systému PMD.
Cílem projektu je vývoj a aplikace originálních moderních numerických metod vhodných pro vysocevýkonné počítače s některými vynikajícími vlastnostmi (numerická a paralelní škálovatelnost) pro výpočty v mechanice tuhé fáze při řešení silně nelineárních problémů. Počítačové kódy jsou vyvíjeny v rámci MKP systému PMD.
Řešitelé: J. Dobiáš, S. Pták, D. Gabriel
Spolupráce: Vysoká škola báňská - Technická univerzita Ostrava
Související publikace:
 Současné znalosti o podmínkách stability a šíření únavových trhlin zatěžovaných v módech II, III a II+III jsou velmi malé ve srovnání se znalostmi pro případ módu I. Cílem projektu jsou nové přístupy k výzkumu chování smykových trhlin, umožňující hlubší poznání mikromechanismů šíření. Naše část projektu je zaměřena na rozsáhlé modelování poškozovacích procesů na čele trhliny metodami 3D molekulární dynamiky. Tato metoda umožňuje získat multiskluzový obraz dislokací a zlepšit klasické dislokační modely.
Současné znalosti o podmínkách stability a šíření únavových trhlin zatěžovaných v módech II, III a II+III jsou velmi malé ve srovnání se znalostmi pro případ módu I. Cílem projektu jsou nové přístupy k výzkumu chování smykových trhlin, umožňující hlubší poznání mikromechanismů šíření. Naše část projektu je zaměřena na rozsáhlé modelování poškozovacích procesů na čele trhliny metodami 3D molekulární dynamiky. Tato metoda umožňuje získat multiskluzový obraz dislokací a zlepšit klasické dislokační modely.
Řešitelé: A. Machová, A. Uhnáková, P. Hora, V. Pelikán, O. Červená
Spolupráce: Fakulta strojního inženýrství, Vysoké učení technické v Brně
Související publikace:
 Naše část projektu je zaměřena na získání nových informací o 3D zdrojích akustické emise vznikajících při prodlužování trhliny, dvojčatění, emisi dislokací a o vlnách u čela trhliny v 3D krystalech alfa železa i jiných kovů zatížených v módu I na atomární úrovni pomocí metody molekulární dynamiky.
Naše část projektu je zaměřena na získání nových informací o 3D zdrojích akustické emise vznikajících při prodlužování trhliny, dvojčatění, emisi dislokací a o vlnách u čela trhliny v 3D krystalech alfa železa i jiných kovů zatížených v módu I na atomární úrovni pomocí metody molekulární dynamiky.
Řešitelé: J. Plešek, A. Machová, A. Uhnáková, P. Hora, V. Pelikán, O. Červená
Související publikace:
 Numerické řešení přechodové úlohy elastodynamiky metodou konečných prvků (MKP) je ovlivněno zvolenou prostorovou a časovou diskretizací. Ta má za následek poškození numerického řešení mimo jiné disperzními chybami, které jsou projevem závislosti fázové a grupové rychlosti na vlnové délce postupující harmonické vlny. Vedle disperzních chyb je možné sledovat mnoho dalších produktů prostorové a časové diskretizace, např. rozptyl směru šíření vln (anizotropie MKP) či exponenciální útlum v prostorových souřadnicích vysokofrekvenčních složek frekvencí z důvodu existence "mtrvých pásem frekvencí", tzv. passing and band gaps. Hlavní pozornost výzkumu je věnována prvkům vyšších řádů (převážně serendipity 20-uzlový isoparametrický konečný prvek) a speciálním volbám tvarových funkcí (spektrální varianta MKP, hierarchické tvarové funkce, spliny, atd. ). Pro zvolené dovolené numerické chyby lze na základě jejich rozboru stanovit meze použitelnosti metody konečných prvků pro numerické řešení úloh šíření elastických vln napětí.
Numerické řešení přechodové úlohy elastodynamiky metodou konečných prvků (MKP) je ovlivněno zvolenou prostorovou a časovou diskretizací. Ta má za následek poškození numerického řešení mimo jiné disperzními chybami, které jsou projevem závislosti fázové a grupové rychlosti na vlnové délce postupující harmonické vlny. Vedle disperzních chyb je možné sledovat mnoho dalších produktů prostorové a časové diskretizace, např. rozptyl směru šíření vln (anizotropie MKP) či exponenciální útlum v prostorových souřadnicích vysokofrekvenčních složek frekvencí z důvodu existence "mtrvých pásem frekvencí", tzv. passing and band gaps. Hlavní pozornost výzkumu je věnována prvkům vyšších řádů (převážně serendipity 20-uzlový isoparametrický konečný prvek) a speciálním volbám tvarových funkcí (spektrální varianta MKP, hierarchické tvarové funkce, spliny, atd. ). Pro zvolené dovolené numerické chyby lze na základě jejich rozboru stanovit meze použitelnosti metody konečných prvků pro numerické řešení úloh šíření elastických vln napětí.
Řešitelé: R. Kolman, J. Plešek, M. Okrouhlík, D. Gabriel
Související publikace:
 Moderní přístup ve výpočtové mechanice je isogeometrická analýza, kde tvarové funkce v MKP diskretizaci jsou založeny na různých typech splinů, např. B-splinů, NURBS, T-splinů a mnoho dalších. Tento přístup zaručuje přesný popis geometrie sledované oblasti a dále pole neznámých veličin (např. pole posuvů) je vyjádřeno stejný způsobem jako geometrie tělesa. Přínosem této prostorové aproximace je spojité pole řešení. Hlavní pozornost výzkumu isogeometrické analýzy je její použití pro numerické řešení úlohy elastodynamiky (vlastní a vynucené kmitání) a dále hlavně pro úlohy šíření elastických vln napětí v tělesech.
Moderní přístup ve výpočtové mechanice je isogeometrická analýza, kde tvarové funkce v MKP diskretizaci jsou založeny na různých typech splinů, např. B-splinů, NURBS, T-splinů a mnoho dalších. Tento přístup zaručuje přesný popis geometrie sledované oblasti a dále pole neznámých veličin (např. pole posuvů) je vyjádřeno stejný způsobem jako geometrie tělesa. Přínosem této prostorové aproximace je spojité pole řešení. Hlavní pozornost výzkumu isogeometrické analýzy je její použití pro numerické řešení úlohy elastodynamiky (vlastní a vynucené kmitání) a dále hlavně pro úlohy šíření elastických vln napětí v tělesech.
Řešitelé: R. Kolman, J. Plešek
Související publikace:
 Projekt se zabývá vývojem a aplikací numerických metod pro přímé řešení velkých systémů lineárních rovnic, které vznikají aplikací metody konečných prvků (MKP) v mechanice kontinua. Systém lineárních rovnic tvoří základ každé MKP úlohy, a proto je nezbytné, aby jeho řešení bylo provedeno rychle a efektivně. To je důležité zejména v metodách řešení nelineárních úloh, kde je třeba matici tuhosti faktorizovat opakovaně. Za velké se považují úlohy, jejichž požadavky na paměťový prostor a výpočetní čas činí řešení náročným na dostupných počítačích. Součástí práce je implementace do konečnoprvkového systému PMD.
Projekt se zabývá vývojem a aplikací numerických metod pro přímé řešení velkých systémů lineárních rovnic, které vznikají aplikací metody konečných prvků (MKP) v mechanice kontinua. Systém lineárních rovnic tvoří základ každé MKP úlohy, a proto je nezbytné, aby jeho řešení bylo provedeno rychle a efektivně. To je důležité zejména v metodách řešení nelineárních úloh, kde je třeba matici tuhosti faktorizovat opakovaně. Za velké se považují úlohy, jejichž požadavky na paměťový prostor a výpočetní čas činí řešení náročným na dostupných počítačích. Součástí práce je implementace do konečnoprvkového systému PMD.
Související publikace:
 Pozornost je věnována především diagonalizaci matice hmotnosti skořepinového prvku typu semiloof, kde je pro potřeby jeho diagonalizace vyvinuto univerzální diagonalizační schéma vycházející ze škálovací metody HRZ. Dále je studována problematika zachování momentu setrvačnosti pro různé typy konečných prvků. Navržené schéma je implementováno do konečněprvkového programu PMD a následně testováno na řadě úloh.
Pozornost je věnována především diagonalizaci matice hmotnosti skořepinového prvku typu semiloof, kde je pro potřeby jeho diagonalizace vyvinuto univerzální diagonalizační schéma vycházející ze škálovací metody HRZ. Dále je studována problematika zachování momentu setrvačnosti pro různé typy konečných prvků. Navržené schéma je implementováno do konečněprvkového programu PMD a následně testováno na řadě úloh.
Řešitelé: V. Sháněl, R. Kolman, J. Plešek
Související publikace: