Viele wichtige industrielle Fertigungsprozesse sowie der Einsatz moderner und funktionaler Materialien sind von Phasenübergängen und Hysterese begleitet. In enger Kooperation mit Anwendern aus Industrie, Physik und Chemie werden am WIAS bereits vorhandene als auch neu entwickelte Modelle im Hinblick auf praxisrelevante Fragestellungen untersucht.

Modellierung von Phasenseparation und Schädigung in modernen Materialien
Die Arbeiten auf diesem Gebiet konzentrieren sich auf die Modellierung von Schädigungsprozessen sowie auf Phasenseparation in modernen Loten der Mikroelektronik.
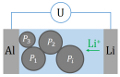
Phasenübergänge und Hysterese im Zusammenhang mit Speicherproblemen
Phasenübergänge und Hysteresen sind charakteristisch für die Energiespeicherung. Ziel ist es, thermodynamische Modelle zur Beschreibung der Speicherprozesse zu formulieren und zu analysieren.
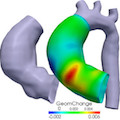
Modellierung, Simulation und Optimierung für Anwendungen in der Biomedizin
In der Medizin werden heute bei der Diagnistik und Therapieplanung digitale Instrumente zur Simulation von Prozessen im menschlichen Körper genutzt. Am WIAS werden Modelle für biologische Gewebe, Fluide und deren Interaktion, sowie Techniken der Optimierung und Steuerung zur Unterstützung von Entscheidungsprozessen in der Biomedizin entwickelt. .

Diffusionsmodelle der Statistischen Physik
Etliche Modelle der Statistischen Physik beinhalten zufällige Pfade mit Interaktionen vielfältiger Natur wie etwa Polymermodelle, bei denen der Pfad eine Selbstabstoßung besitzt sowie attraktive Interaktionen mit dem umgebenden Raum, Massetransportmodelle, bei denen der Pfad eine zufällige Masse trägt, die abhängig von den Eigenschaften des besuchten Raumes zufällig vergrößert oder verkleinert wird, oder Selbstüberschneidungseigenschaften zufälliger Pfade.
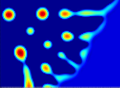
Modellierung dünner Filme und Nanostrukturen auf Substraten
Dünne Filme spielen eine wichtige Rolle in der Natur und vielen technologischen Anwendungen. Insbesondere im Mikro- und Nanometerbereich werden zum Beispiel Entnetzungsprozesse oder epitaktisches Wachstum zum Design von Oberflächen mit spezifischen Materialeigenschaften eingesetzt. Neben der Bedeutung, die die mathematische Modellierung, Analysis und numerische Simulation für die Beschleunigung der Entwicklung neuere Technologien hat, ist es auch wissenschsftlich auch äußerst interessant Materialeigenschaften auf diesen kleinen Skalen zu verstehen.
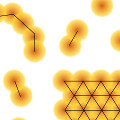
Partikelbasierte Modellierung in den Naturwissenschaften
Seit über hundert Jahren ist die Modellierung mit Hilfe von vielen zufälligen Partikeln eine übliche Herangehensweise an das Studium von Vorgängen und Phänomenen in den Naturwissenschaften. Daher wurden und werden immer mehr Modelle aufgestellt und mathematisch analysiert, die auf mikroskopischer Ebene durch eine große Anzahl von Teilchen und einer Formulierung der Regeln der Wechselwirkungen zwischen ihnen definiert werden.

Nichtlineare Materialmodelle, multifunktionale Materialien und Hysterese im Zusammenhang mit elasto-plastischen Prozessen
Die Funktionsweise vieler Komponenten in moderneren Geräten beruht auf spezifischen Eigenschaften so genannter multifunktionaler Materialien. Diese Materialien zeichnen sich dadurch aus, dass darin Eigenschaften wie elastische Verformbarkeit, thermische Ausdehnbarkeit, Magnetisierbarkeit oder Polarisierbarkeit auf nichttriviale Weise miteinander wechselwirken, wie zum Beispiel in Piezo-Kristallenen. Am WIAS werden hierzu gekoppelte Modelle entwickelt und analysiert.
Hauptanwendungsgebiete
Ansprechpartner
Beteiligte Gruppen
- Partielle Differentialgleichungen
- Numerische Mathematik und Wissenschaftliches Rechnen
- Nichtlineare Optimierung und Inverse Probleme
- Stochastische Systeme mit Wechselwirkung
- Thermodynamische Modellierung und Analyse von Phasenübergängen
- Nichtglatte Variationsprobleme und Operatorgleichungen
- Numerische Methoden für innovative Halbleiter-Bauteile
- Modellierung, Analysis und Skalenübergänge von Volumen-Grenzschicht-Prozessen


