Nano- und Optoelektronik

Optische Technologien sind eine der wichtigsten Zukunftsbranchen des 21. Jahrhunderts und tragen wesentlich zum technologischen Fortschritt bei. Sie sind nicht zuletzt wegen der resultierenden innovativen Infrastruktur unverzichtbar für eine weitere Digitalisierung von Industrie, Wissenschaft und Gesellschaft.

Durch mathematische Modellierung, numerische Simulationen sowie durch theoretisches Verständnis der auftretenden Effekte leistet das WIAS dabei einen wichtigen Beitrag zur technologischen Weiterentwicklung. Ein Schwerpunkt dieses Anwendungsthemas ist hierbei die Modellierung und mathematische Analysis der auftretenden Gleichungen, sowie die numerische Simulation von Halbleiterbauelementen.

Zu den Themenschwerpunkten zählen:

• organische Halbleiter (z. B. organische Leuchtdioden)
• Anwendungen aus der Laser-Technologie sowie Probleme aus der nichtlinearen Faseroptik
• mathematische Optimierung optoelektronischer Bauteile (Silicon Photonics)
• quantenmechanische Modellierung von Nanostrukturen und ihre konsistenten Kopplung an makroskopische Modelle
• Hybridmodellierung von Halbleiterbauteilen sowie "Bulk-Interface" Prozesse
• effiziente Algorithmen in der diffraktiven Optik für die Simulation der Streuung an neuen komplexeren nanostrukturierten Oberflächen

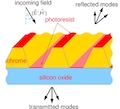
Anwendungen in der diffraktiven Optik

Diffraktive optische Elemente basieren auf Beugungseffekten an mikrostrukturierten Grenzflächen. Sie ermöglichen die Realisierung neuer Abbildungsfunktionen und neuer optischer Bauteile z.B. in der diffraktiven Messtechnik, in Spektroskopie, Astronomie, optischer Kommunikation und Informationsverarbeitung. Für das Design dieser Elemente werden die Maxwellschen Gleichungen gelöst und spezielle Optimierungsalgorithmen eingesetzt.

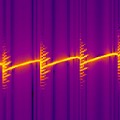
Dynamik von Halbleiterlasern

Halbleiterlaser sind kompakte, effiziente und zuverlässige Lichtquellen und stellen Schlüsselkomponenten für zahlreiche, moderne technologische Anwendungen dar. In Abhängigkeit von den verwendeten Halbleitermaterialien sowie den Geometrien der Bauelemente weisen diese Lasersysteme eine Vielzahl komplexer dynamischer Zustände auf. Diesen liegen nichtlineare Prozesse und Bifurkationen zugrunde, die umfassend untersucht werden müssen. Erst durch deren Verständnis wird die Entwicklung neuer, anwendungsspezifischer Bauelemente möglich.

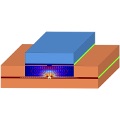
Modellierung und Simulation von Halbleiterstrukturen

Moderne Halbleiter- und Optoelektronik wie Halbleiterlaser oder organische Feldeffekttransistoren basieren auf Halbleiterstrukturen, die z.B. durch Dotierungsprofile, Heterostrukturen oder Nanostrukturen gegeben sein können. Um das Verhalten dieser Bauelemente qualitativ und quantitativ zu beschreiben und zu optimieren, ist die mathematische Modellierung und Simulation der funktionsbestimmenden bzw. -limitierenden Ladungstransportvorgänge notwendig. Im Rahmen der Green Photonics Initiative stehen auch energieeffizientere Bauteile sowie neue Anwendungen im Bereich der erneuerbaren Energien, Kommunikationstechnologien und Beleuchtung im Vordergrund.

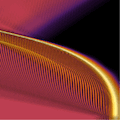
Pulse in optisch nichtlinearen Medien

Gegenstand dieses Anwendungsthemas aus dem Bereich der extrem nichtlinearen Optik ist die Untersuchung und Beschreibung intensiver ultrakurzer Laserpulse in optischen Fasern. Im Mittelpunkt steht hierbei die Entwicklung neuer, numerisch effektiver Modelle, die die Ausbreitung und Stabilität dieser Pulse beschreiben und zugleich sowohl die zeitlich nichtlokale Medien-Response als auch physikalische Grundprinzipien korrekt berücksichtigen. Von besonderer Bedeutung ist dabei u.a. das Kausalitätsprinzip, das zu den intrinsischen Kramers-Kronig-Beziehungen zwischen Dispersion und Dissipation führt.

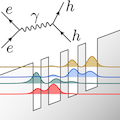
Quantenmechanische Modelle für Halbleiter

Die relativ großen Abmessungen von Halbleiterbauteilen und die Komplexität quantenmechanischer Modelle erfordern die konsistente Modellierung von klassischer und quantenmechanischer Beschreibung durch sogenannte Hybridmodelle, z.B. durch Kopplung des Drift-Diffusions-Modells mit Quanten-Mastergleichungen in Lindblad-Form zur Beschreibung eingebetteter offener Quantensysteme. Solche Hybridsysteme ermöglichen die Modellierung komplexer Bauelemente wie Quantenpunkt-Lasern oder Einzelphotonenemittern.