Many important processes of industrial production and use of modern and functional materials are accompanied by phase transitions and hysteresis. In tight collaboration with users from industry, physics and chemistry existing as well as newly developed models are studied at WIAS regarding their practical relevance.
Modeling of phase separation and damage in modern materials
This work is focussed on the modeling of damage and on phase separation in modern solder materials for microelectronic devices.
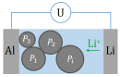
Phase transition and hysteresis in the context of storage problems
Phase transitions and hysteresis are characteristics of energy storage problems. The aim is to formulate and analyse a thermodynamical model which discribes the storage problem.
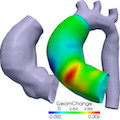
Modeling, Simulation and Optimization for Biomedical Applications
Today, in medical science digital simulation instruments for processes in the human body are utilized in diagnistics and therapy planning. At WIAS, models for biological tissues, fluids, and their interaction as well as techniques in optimization and optimal control for decision support in biomedicin are devloped.

Diffusion models in statistical physics
Many models in statistical physics contain random paths with interactions of various natures, like polymer models, where the path has a self-repellence and attractive interactions with the surrounding medium, mass transport models, where the path carries a random mass that is increased and decreased, depending on the properties of the space visited, or self-intersection properties of the path.
Modeling of thin films and nano structures on substrates
Thin films play an important role in nature and many areas of technological applications. In particular on micro- and nanoscales technological processes such as dewetting or epitaxial growth are used to design surfaces with specific material properties. Apart from the need to derive mathematical decriptions, analyis and numerical simulation, that serve to accelerate the development of new technologies, it is also exciting to understand material behaviour on these small scales.
Particle-based modeling in the Sciences
For more than a hundred years diverse processes and phenomena in the natural sciences have been modelled using random particle systems. As a result ever more models that specify a large number of particles and rules for how they interact have been both proposed and mathematically analysed.

Nonlinear material models, multifunctional materials and hysteresis in connection with elasto-plastic processes
Many components in modern equipment rely on specific properties of so-called multifunctional materials. These materials are distinguished by the fact that therein properties like elastic deformability, thermal expansibility, magnetizability, or polarizability interact nontrivially like for instance in a piezo-crystal. At WIAS coupled models describing these properties are developed and analyzed.
Main Areas of Application
Contact
Contributing groups
- Partial Differential Equations
- Numerical Mathematics and Scientific Computing
- Nonlinear Optimization and Inverse Problems
- Interacting Random Systems
- Thermodynamic Modeling and Analysis of Phase Transitions
- Nonsmooth Variational Problems and Operator Equations
- Numerical Methods for Innovative Semiconductor Devices
- Modeling, Analysis, and Scaling Limits for Bulk-Interface Processes


