Novinky
Na čem pracujeme: Turbulence plazmatu a kinetické nestability v expandujícím slunečním větru
Jako sluneční vítr souhrnně označujeme neustálý proud částic od Slunce do nitra Sluneční soustavy. Jeho popis i matematické modelování procesů v něm probíhajících je jádrem výzkumu skupiny Heliosféry a kosmického počasí Slunečního oddělení ASU. Ve své poslední práci se věnovali modelování turbulence plazmatu na mikroskopických škálách a popisují energetickou kaskádu transformující energii přítomnou na největších škálách do energie jednotlivých částic.
Turbulence v magnetizovaném nízkosrážkovém plazmatu zůstává jedním z nevyřešených problémů fyziky plazmatu. Materiál v kosmickém prostoru, zejména pak sluneční vítr, je tak unikátní laboratoří umožňující studium těchto procesů. Ukazuje se, že v takovém prostředí je turbulence velmi nelineárním problémem, který umožňuje přenos energie od velkých prostorových škál k jednotlivým částicím.
V tom činí i problém této disciplíny. Turbulentní chování na velkých rozměrových škálách lze postihnout tzv. magnetohydrodynamickým (MHD) přístupem, kdy se k plazmatu přistupuje jako k zmagnetizované tekutině. Tento zjednodušující přístup má překvapivě cenné výsledky. Popisuje například celý komplex vln, které se plazmatem šíří. Ve slunečním větru mezi nejdůležitější patří speciální typ magnetohydrodynamických vln, tzv. vlny Alfvénovy. Ty popisují typický způsob šíření poruch magnetického pole. Pro popis dějů na menších škálách, na nichž se již projevují efekty jednotlivých částic, je však MHD přístup nedostačující. Na těchto škálách se očekává kaskádní přenos energie z velkých rozměrů. O tomto přenosu svědčí některé vlastnosti slunečního větru. Např. měřené radiální profily protonové teploty jsou důkazem o radiálním ohřevu protonů, do nějž vstupuje energie porovnatelná právě s energií turbulentní kaskády. Očekává se, že tento energizační proces by mohl mít zpětnou vazbu na samotnou velkorozměrovou turbulenci. Ve slunečním větru situaci nadále komplikuje jeho neustálá expanze, která do procesu přináší naopak útlum. Expanze tedy turbulentní kaskádu zpomaluje. A v neposlední řadě se kvůli „ředění“ látky částicové škály se vzdáleností od Slunce mění, což nejspíše proces energizace částic opět komplikuje.
P. Hellinger a jeho kolegové situaci matematicky modelovali s pomocí hybridního popisu, v němž se řeší pohyby a vlastnosti pouze iontů, zatímco elektrony jsou považovány za nehmotné fluidum sloužící pouze k vyrovnání náboje, aby byla zachována elektrická neutralita látky. To není nijak divoké přiblížení, neboť elektrony jsou reálně tisíckrát méně hmotné než protony. Problém byl řešen pouze ve dvou dimenzích kolmých na pozaďové magnetické pole a na radiální směr. V těchto dvou tranversálních směrech ovlivňovala dění také celková expanze.
V simulaci vystupovalo 1024 makročástic na výpočetní buňku hrajících roli shluků protonů. Jejich kolektivní chování bylo nastaveno tak, aby časoprostorové spektrum bylo izotropní se zastoupením modů s náhodnou fází, lineární Alvénovskou polarizací (tedy že magnetické pole poruchy bylo vždy kolmé na vektor intenzity pozaďového pole) a s nekorelovanými poruchami magnetického pole a rychlosti částic. Systém se nechal vyvíjet podle fyzikálních rovnic.
Vývoj ukazuje, že počáteční náhodné poruchy velmi rychle relaxují a vyvíjí se turbulentní kaskáda, tedy původní ploché spektrum se mění na mocninnou funkci. Směrnice této funkce se však náhle mění u iontové škály. Celková amplituda spektra s časem klesá kvůli expanzi výpočetního boxu a také turbulentním tlumením.
V první fázi vývoje tedy systém relaxuje, zvětšují se poruchy magnetického pole na úkor poruch rychlostí. V druhé fázi dojde k turbulentnímu ohřevu protonů především v kolmém směru. Celkově však teplota protonů klesá, neboť turbulentní ohřev je méně významný než pokles teploty v důsledku expanze výpočetního boxu a protony získávají podstatnou teplotní anizotropii, podobně jako je tomu ve slunečním větru. V systému se však objevují kinetické nestability, konkrétně “hadicová” (firehose) nestabilita. Tato nestabilita nese svůj název po hasičské hadici a to právem. Necháme-li na zemi položenou rovnou hadici s proudící vodou, existuje v systému silná anizotropie (voda proudí pouze podél hadice, nikoli v kolmém směru). Stačí pak malá porucha a hadice se začne “kroutit jako had”. V našem idealizovaném systému se objevují komponenty rychlosti kolmo na původní směr. Hadicová nestabilita tedy omezuje anizotropii protonů a ovlivňuje i charakter turbulence.
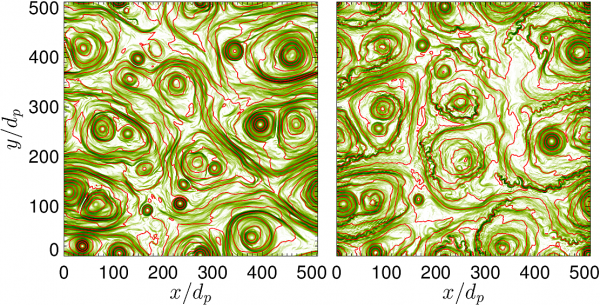
Tato teoretická práce tedy ukazuje, že kinetické nestability mohou koexistovat se silnou turbulencí plazmatu dokonce i v 2-D režimu. K přímé aplikaci na chování plazmatu slunečního větru je však ještě daleko. Pro to je potřeba simulaci zobecnit do 3-D, což s sebou nese mimojiné vyšší výpočetní náročnost.
Michal Švanda
Citace práce
Hellinger, P. a kol., Plasma turbulence and kinetic instabilities at ion scales in the expanding solar wind, Astrophysical Journal Letter (2015) 811, L32 (2015), arXiv:1508.03159
Kontakt: Dr. Mgr. Petr Hellinger, petr.hellinger@asu.cas.cz