Novinky

Na čem pracujeme: Dynamika slunečního větru v numerické simulaci

Vnitřní část Sluneční soustavy je vyplněna neustálým proudem částic pocházejících ze Slunce, tzv. slunečním větrem. Byť byly základy teorie slunečního větru položeny v šedesátých letech minulého století, dodnes je tento jev opředen mnoha tajemstvími. Omezená dostupnost pozorování neumožňuje v tuto chvíli plně vysvětlit komplexitu proudění plazmatu od Slunce, ke slovu tedy přicházejí numerické simulace. Petr Hellinger z ASU ve své práci představuje výsledky zaměřené na studium turbulence a nestabilit ve slunečním větru.

Z hlediska teorie plazmatu lze sluneční vítr považovat za turbulentní slabě srážkové prostředí a jako takové je zajímavou přírodní laboratoří výzkumu turbulence. Vlastnosti turbulentního proudění zůstávají i pro dnešní fyziku velkou výzvou a tím méně jsou uchopeny popisy turbulence v plazmatu, tedy plynu s velkým množství elektricky nabitých částic, které vykazují v přítomnosti magnetických a elektrických polí kvalitativně jiné chování než elektricky neutrální částice běžných plynů. Z pohledu velkých rozměrů si lze při popisu slunečního větru vystačit s tzv. magnetohydrodynamickým (MHD) přístupem, který přistupuje k plazmatu jako k tekutině a odhlíží od jevů, ke kterým dochází na mikroskopických škálách. MHD popis tak mnohé jevy není vůbec schopen interpretovat.

Pozorovací data jsou obvykle k dispozici z in-situ experimentů přímo na kosmických družicích, tyto údaje však charakterizují vlastnosti slunečního větru pouze jednorozměrně podél trajektorie družice. Kombinací různých jednorozměrných dat lze dát dohromady ne zcela detailní obrázek o charakteru větru v různých vzdálenostech od Slunce. Z těchto údajů například vyplývá, že vlastnosti elektricky nabitých částic – například protonů – často závisejí na směru vůči pozaďovému magnetickému poli (jsou tzv. anizotropní). Podél a napříč pole jsou například identifikovány různé teploty. Prostorové změny vlastností často vedou ke vzniku nejrůznějších typů nestabilit, které mohou zpětně ovlivňovat mikroskopické i makroskopické vlastnosti větru. Celou situaci ještě komplikuje fakt, že díky rozpínání slunečního větru do prostoru se vzdáleností od Slunce se charakter turbulence mění. S expanzí jsou turbulentní změny tlumeny. Rozpínání ale vytváří v systému další preferovaný směr, v němž se mění charakteristické mikroskopické vlastnosti částic. Numerické simulace naznačují, že v takových podmínkách vzniká celá turbulentní kaskáda, v níž se přelévá energie mezi jednotlivými prostorovými škálami. Rozpínání posiluje teplotní anizotropie částic.

Petr Hellinger z ASU byl vedoucím autorem studie, na níž se podíleli i další vědci ze světových institucí. Cílem bylo studium výsledků realistické numerické simulace tzv. hybridním kódem v expandujícím boxu. Řešení bylo plně trojrozměrné, což zvyšuje jeho věrohodnost proti předchozím studiím prováděným v méně rozměrech. Kód je hybridní v tom, že zachází odlišně s těžkými a lehkými částicemi. A tak zatímco těžké protony jsou řešeny na částicové úrovni, lehké elektrony jsou brány zjednodušeně jako pozaďová tekutina, jejímž jediným účelem je neutralizovat lokální elektrické náboje protonů. Tento přístup je ve fyzice plazmatu využíván poměrně často. Kartézský (pravoúhlý) výpočetní box připouštěl časový vývoj (expanzi) dvou souřadnicových os, čímž se připodobnila situace v reálném expandujícím slunečním větru rozpínajícím se v transverzálních směrech. Rozpínání je parametrizováno charakteristickým expanzním časem, který odpovídá času, za nějž do daného místa dorazí sluneční vítr konstantní rychlostí. Dynamika byla ve výpočetním boxu iniciována izotropním trojrozměrným spektrem vln s náhodně zvolenými fázemi, jejichž magnetické fluktuace dosahovaly rozptylu s hodnotou asi čtvrtiny hodnoty magnetické indukce pozaďového pole. Aby autoři zabránili akumulaci kaskádující turbulentní energie na škálách odpovídajících jemnosti výpočetní sítě, předepsali plazmatu tlumící faktor (rezistivitu) s nízkou hodnotou.

Autoři pak s napětím studovali časový vývoj plazmatu v takovém prostředí. V počátku vývoje významně narostla celková úroveň magnetických fluktuací, jak se v systému utvářela turbulentní kaskáda a část kinetické energie protonů se transformovala v energii magnetického pole. Po této krátké úvodní epizodě však fluktuace magnetického pole klesly a poruchy magnetické pole drobně oscilovaly kvůli superpozici pohybujících se velkoškálových Alfvénových vln. Amplituda elektrického proudu se měnila podobně a též svědčila pro přítomnost dobře rozvinuté turbulentní kaskády. Také teplotní anizotropie protonů má od začátku simulace tendenci spíše klesat. Chování se však mění v čase kolem 0,14 charakteristického času expanze, kdy teplotní anizotropie epizodicky roste, stejně jako se zvětšují podélné fluktuace magnetického pole, což souvisí s výskytem vln s výraznou podélnou komponentou. Turbulentní kaskáda vytváří rychlostní střih na iontových škálách a tím přirozeně vytváří teplotní anizotropii. Energizace protonů ale není dostatečná, aby mohla konkurovat anizotropnímu chlazení v důsledku expandujícího výpočetního boxu. Redukce teplotní anizotropie po čase kolem 0,15 charakteristického času expanze svědčí pro vznik hadicové nestability. Ta vzniká v případě anizotropního proudění, kdy je proudění podél náchylné ke kolmým poruchám a snadno tak změní směr. Hadicovou nestabilitu zná každý uživatel vysokotlakých hadic, která se za určitých podmínek, proudí-li jí tekutina, může stát „divoce se kroutícím hadem“ na zemi.

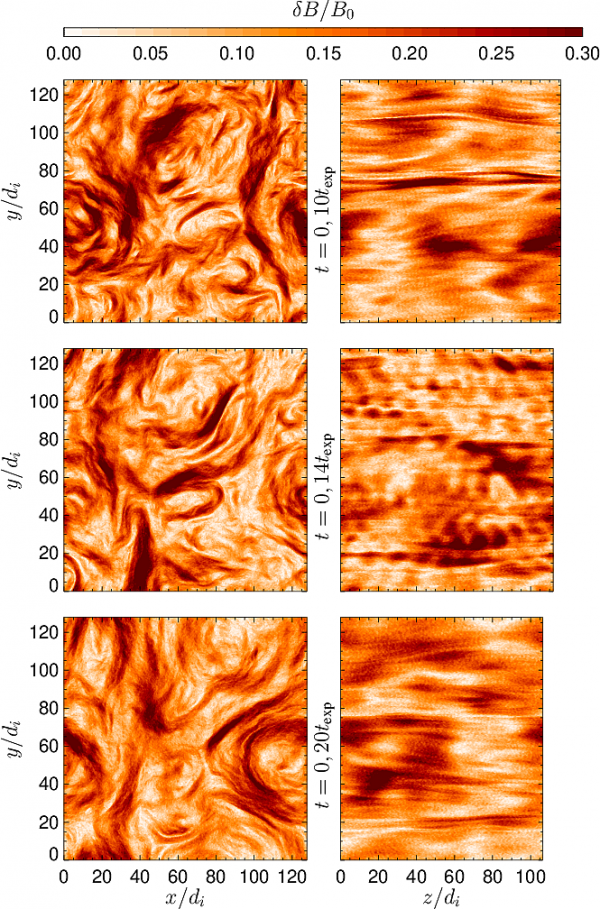
Jakmile je protonová teplotní anizotropie dostatečně silná, hadicová nestabilita se destabilizuje a vznikají vlnové balíčky s velmi malými amplitudami ve srovnání s amplitudou fluktuací pozaďového pole. Vygenerované vlny velmi efektivně redukují protonovou teplotní anizotropii, vlny jsou částečně znovu absorbovány protony a částečně se podílejí na rozvoji turbulentní kaskády.

Otázkou zůstává, zda je možné chování popsané v simulaci pozorovat v reálném slunečním větru přístroji kosmických sond. Autoři tedy v simulaci udělali jednorozměrné řezy a konstatují, že výskyt fluktuací souvisejících s hadicovou nestabilitou by mělo být možné odhalit z výkonových spekter vypočtených pro podélnou komponentu vektorových fyzikálních veličin (např. rychlosti nebo magnetické indukce). Tyto fluktuace se nacházejí v jiné části disperzního diagramu než fluktuace pozaďového pole, takže je možné je z pozorování odlišit. Pokud by však sonda prolétala ve více skloněném úhlu vůči směru magnetického pole, aktivita hadicové nestability by byla nerozpoznatelná.

Numerické simulace mají své limity, plynoucí z jejich samotné podstaty, představují ale zajímavý materiál pro studium jevů, které je jinak obtížné pozorovat přímo. Validitu těchto simulací ale lze ověřit jedině pozorováním. Numerické simulace dávají také předpovědi na to, co lze realisticky očekávat v pozorováních a také návod na jejich plánování.

Michal Švanda

Citace práce

P. Hellinger a kol., Turbulence vs. fire hose instabilities: 3-D hybrid expanding box simulations, Astrophysical Journal v tisku, preprint arXiv:1908.07760

Kontakt: Dr. Mgr. Petr Hellinger, petr.hellinger@asu.cas.cz