Solution: Denote by x the radial coordinate, r=1m the
inner radius, rY the radius of plastic zone, and R=2m the outer
radius of the tube, respectively. The elastic solution valid in the domain
 satisfying
satisfying
 at the boundary takes the form
at the boundary takes the form
![\begin{displaymath}
\begin{array}{rcl}
\sigma_r&=&C[1-\left(\frac{R}{x}\right)^2...
...}{x}\right)^2]\\
\sigma_o&=&\nu(\sigma_r+\sigma_t)
\end{array}\end{displaymath}](img229.gif) |
(V.1) |
C is a constant to be determined from the yield condition
 .
Substituting (V.1) into
von Mises' function
.
Substituting (V.1) into
von Mises' function  with x=rY, we get
with x=rY, we get
![\begin{displaymath}
C(r_y)=\sigma_Y
\left[(1-2\nu)^2+3\left(\frac{R}{r_Y}\right)^4\right]^{-\frac{1}{2}}
\end{displaymath}](img232.gif) |
(V.2) |
A closed form solution in the plastic zone x<rY can only be obtained
for Tresca's condition or if  .
With von Mises's criterion and
.
With von Mises's criterion and
 we must resort to some simplifying assumptions.
we must resort to some simplifying assumptions.
The state of plane strain enforces
![\begin{displaymath}
\epsilon_o=\epsilon_o^e+\epsilon_o^p=
\frac{1}{E}[\sigma_o-\nu(\sigma_r+\sigma_t)]+\epsilon_o^p=0
\end{displaymath}](img234.gif) |
(V.3) |
At the elastic-plastic interface we have
 ,
which gives
,
which gives
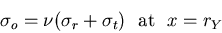 |
(V.4) |
If the loading approaches its plastic limit, the stress components cease
to change, therefore
 and (V.3)
requires that
and (V.3)
requires that
 .
Using the Prandtl-Reuss
equations
.
Using the Prandtl-Reuss
equations
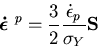 |
(V.5) |
and calculating the axial component of deviatoric stress tensor  we derive
we derive
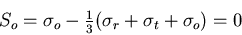 |
(V.6) |
Hence
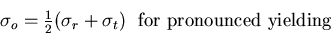 |
(V.7) |
Equations (V.4) and (V.7) suggest that the axial
stress is bounded in the plastic zone by
 |
(V.8) |
when
 at x=rY whereas the upper bound
is approached in a limit as
at x=rY whereas the upper bound
is approached in a limit as
 .
.
Now, an approximation to the yielding function  is made by assuming
is made by assuming
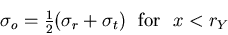 |
(V.9) |
Setting
 we obtain the yield condition in the form
we obtain the yield condition in the form
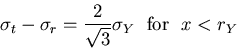 |
(V.10) |
In view of (V.4) the maximum deviation should be expected in
the vicinity of the elastic-plastic boundary. The error can easily be
estimated by inserting elastic solution (V.1), (V.2)
into the expression
![\begin{displaymath}
\sigma_t-\sigma_r=2\sigma_Y
\left[(1-2\nu)^2\left(\frac{R}{r_Y}\right)^4+3\right]^{-\frac{1}{2}}
~~\mbox{at}~~x=r_Y
\end{displaymath}](img247.gif) |
(V.11) |
Clearly, if  the right-hand sides of (V.10) and
(V.11) are coincident. In this example
the right-hand sides of (V.10) and
(V.11) are coincident. In this example  ,
R/rY=2/1.5, thus
,
R/rY=2/1.5, thus
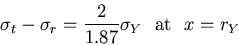 |
(V.12) |
Comparison with the factor
 shows that (V.10) is a
good approximation to the yield condition at any point in the plastic
zone.
shows that (V.10) is a
good approximation to the yield condition at any point in the plastic
zone.
Solving the equilibrium equations
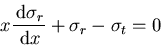 |
(V.13) |
together with (V.10) and the boundary condition
 yields
yields
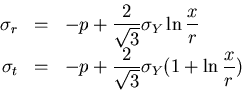 |
(V.14) |
The relationship between p and rY can be established by equating
(V.1)1 and (V.14)1 at x=rY, from which
![\begin{displaymath}
\frac{p}{\sigma_Y}=
\left[\left(\frac{R}{r_Y}\right)^2-1\rig...
...t)^4\right]^{-\frac{1}{2}}
+\frac{2}{\sqrt{3}}\ln\frac{r_Y}{r}
\end{displaymath}](img254.gif) |
(V.15) |
In this example we choose rY=1.5m, thus
 MPa.
MPa.
The estimate of  given by (V.9) is satisfactory for
the approximation of the yielding function but it would have been very
inaccurate for the calculation of
given by (V.9) is satisfactory for
the approximation of the yielding function but it would have been very
inaccurate for the calculation of
 .
Fortunately, a
second-order correction can now be introduced by applying the
Prandtl-Reuss equations.
.
Fortunately, a
second-order correction can now be introduced by applying the
Prandtl-Reuss equations.
We use (V.9) and (V.14) as a first approximation to
compute the deviatoric stress
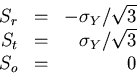 |
(V.16) |
Since the deviator is independent of plastic strain the Prandtl-Reuss
equations (V.5) may easily be integrated
 |
(V.17) |
By virtue of (V.3) the total strain components are computed as
![\begin{displaymath}
\begin{array}{rcl}
\epsilon_r &=&\displaystyle\frac{1-\nu^2}...
...\sigma_r]+\displaystyle\frac{\sqrt{3}}{2}\epsilon_p
\end{array}\end{displaymath}](img260.gif) |
(V.18) |
and substituted into compatibility condition
 |
(V.19) |
With the aid of (V.14) and after some manipulations the
differential equation for cumulated plastic strain
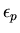 is
obtained
is
obtained
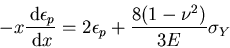 |
(V.20) |
Solving (V.20) with the boundary condition
 we arrive at
we arrive at
![\begin{displaymath}
\epsilon_p=\frac{4(1-\nu^2)}{3E}\sigma_Y
\left[\left(\frac{r_Y}{x}\right)^2-1\right]
\end{displaymath}](img264.gif) |
(V.21) |
Once the cumulated plastic strain has been calculated we receive a better
estimate of
 .
Integration of the Prandtl-Reuss equations
(V.5) leads to
.
Integration of the Prandtl-Reuss equations
(V.5) leads to
![\begin{displaymath}
\epsilon_o^p=\frac{1}{\sigma_Y}\int_0^{\epsilon_p}
[\sigma_o...
...}{\sigma_Y}[\sigma_o-\textstyle\frac{1}{2}(\sigma_r+\sigma_t)]
\end{displaymath}](img266.gif) |
(V.22) |
Finally,  is resolved from (V.3) as
is resolved from (V.3) as
 |
(V.23) |
Note that
 if
if
 and
and
 as
as
 .
.
The results of numerical analysis and the analytical solution described
by eqns. (V.1),(V.2), (V.14) and
(V.23) are shown in figure.

![]() is made by assuming
is made by assuming
![]() given by (V.9) is satisfactory for
the approximation of the yielding function but it would have been very
inaccurate for the calculation of
given by (V.9) is satisfactory for
the approximation of the yielding function but it would have been very
inaccurate for the calculation of
![]() .
Fortunately, a
second-order correction can now be introduced by applying the
Prandtl-Reuss equations.
.
Fortunately, a
second-order correction can now be introduced by applying the
Prandtl-Reuss equations.
![]() .
Integration of the Prandtl-Reuss equations
(V.5) leads to
.
Integration of the Prandtl-Reuss equations
(V.5) leads to
